
(ドナルド・ルービン教授と筆者。筆者撮影)
因果関係を理解したり、証明したりするには考え方の体系的な枠組み(フレームワーク)が必要です。ある2つの事象が因果関係にあると主張するのは勝手かもしれませんが、それが事実なのか、それとも”言い張っているだけ”なのかを判断するためには、それを評価するためのルールが必要になります。どんな条件を満たせば因果関係にあると証明することができて、何が足りないと因果関係を述べることができないのか、を理解しましょう。学問の分野によって考え方はまちまちです。ここでは、専門分野に関わらず普遍的な因果推論(因果関係にあるということを証明する方法)の考え方を理解するために、(1)統計学(ルービン)、(2)心理学(キャンベル)、(3)疫学(パール)の3つの分野における因果推論を順番に説明し、必要に応じて対比させていきたいと思います。今回はその中でも(1)統計学における因果推論に関してお話します。
(1)統計学における因果推論(ルービンの因果モデル)
因果推論の中でも最も有名なものの一つが「ルービンの因果モデル」であると言っても過言ではないと思います。これはハーバード大学の統計学者ドナルド・ルービンが1970年代半ばに開発した方法論です。ルービンは因果関係でもっとも有名ですが、これ以外にもデータに欠損値があるとの統計解析方法である多重代入法(Multiple imputation method)や、そのままでは比較可能ではない観察データから比較可能な2群を作り出すプロペンシティスコア法(Propensity score method)を開発したことでも有名です。
ルービンの因果モデルを理解するうえで最も重要なコンセプトはPotential outcome(潜在的なアウトカム)です。ルービンの因果モデルは、イェジ・ネイマンとロナルド・フィッシャーという2人の偉大な統計学者の業績の上に成り立っています。1923年にPotential outcomeというコンセプトを初めて提唱したのはネイマンです(18世紀の哲学者デイビッド・ヒュームがほのめかしていましたが、きちんと概念化したのはネイマンです)。そして、フィッシャーは1920年代半ばに因果推論におけるランダム化比較試験(RCT)の重要性と説いていましたが、なぜRCTでないと正しい因果推論ができないのかをきちんと説明することができませんでした。ルービンの因果モデルを用いることで、はじめてなぜRCTが因果推論に最適なのか、そしてどんな条件が揃えば観察研究データからも正しく因果推論を行うことができるのかが説明できるようになったとされています。そしてルービンの因果モデルが一躍有名になったのは、Hollandの1986年の論文であると言われています。
ルービンの因果モデルの基本的な考え方は、各個人において、治療を受けた場合と受けなかった場合の両方のアウトカムが観察できれば、その差を取ることで個人レベルでのTreatment effect(治療効果)が推定できる、という点から始まります。そしてその個人レベルの治療効果の平均値を取ることで、「サンプルに含まれる人すべてが治療を受けた場合」と「サンプルに含まれる人すべてが治療を受けなかった場合」の差を見ることができ、これが集団レベルでの介入効果(平均介入効果)になります。
例を用いてご説明します。日本では2014年4月1日より消費税が5%から8%に増えました。そして2014年7~9月の四半期GDP成長率は実質-0.4%(名目-0.8%)でした。新聞やテレビでは有識者や政治家は消費税引き上げがマイナス成長の原因である、という議論を展開していますが、これはまさに「因果推論」の話になります。4月に消費税を引き上げた場合のGDP成長率と、引き上げなかった場合のGDP成長率の両方を観察することができれば、その差が消費税引き上げのTreatment effectになります。実際には消費税は引き上げられたのですが、もしタイムマシンを使って2014年3月まで戻って、どうにか消費税引き上げを思いとどまらせて、そしてその後のGDP成長率を見て、その差を取ることができれば因果関係を証明できます。
この消費税引き上げがあった場合となかった場合の、それぞれのパターンにおけるアウトカム(この場合はGDP成長率)のことをPotential outcome(潜在的な結果)と呼びます。経済学や疫学におけるCounterfactual(反事実)と同じコンセプトであると考えて頂ければよいと思います。(正確には2つの概念は少しだけ違います。Potential outcomeは観察されたアウトカムと観察されなかったアウトカムの両方のことを指します。一方で、Counterfactualは観察されなかった方のアウトカムのことを指し、それに対して観察された方のアウトカムはFactualと呼ばれます)。
ここで問題になるのは、実際にはタイムマシンが存在しないということです。そのため、実世界ではPotential outcomeのうち、片方(実際に起こった方)のアウトカムしか観察することができず、もう片方のアウトカムは常に欠損データとなってしまうことです。つまり、ルービンは、「因果推論とは根本的に“欠損データ”の問題である」と考えました。これを理解すると、なぜルービンが欠損のあるデータの解析方法であるMultiple imputationを開発したのを理解して頂けると思います。
Potential outcomeの概念を理解し、データを解析するために、ルービンは科学(Science)と呼ばれる表を使っています。下の表がScienceになります。例を用いてご説明します。降圧薬を飲んだ人と飲んでいない人を比べて、その収縮期血圧を見たデータがあるとします。ここでは降圧薬を飲んでいた場合には治療=1、飲んでいない場合には治療=0となります。そして降圧薬を飲んだ場合と、飲まなかった場合の血圧の値をそれぞれY(1)とY(0)とします。このY(1)とY(0)がPotential outcomeです。
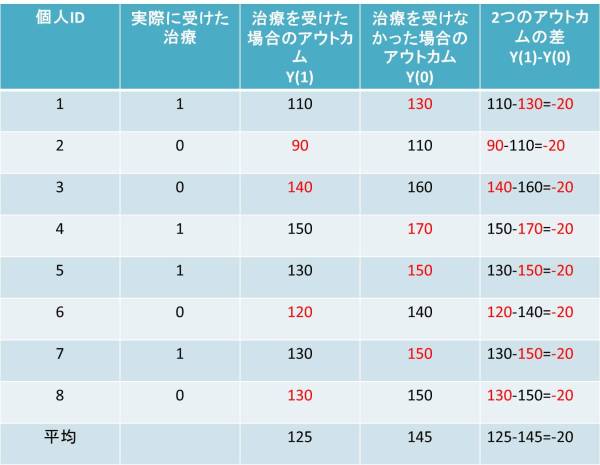
表1:各人で治療を受けた場合と受けなかった場合の両方のアウトカムが観察できた場合
表2:実際に観察できるアウトカム
理想的には、表1のように、各人において降圧薬の有無の両パターンにおける血圧の値が観察できれば、個々人での降圧薬の効果を判定することができます。これを集計すれば、降圧薬の効果は、収縮期血圧を20 mmHg下げることが分かります。この表において赤字で示されているところは、実際には観察できないアウトカムになります。一人目の患者さんは実際に治療を受けたのでY(1)しか観察できませんし、二人目の患者さんは降圧薬を実際には飲んでいないのでY(0)しか観察できません。そうなると現実世界では、表2のように欠損値(「?」で示してあります)だらけになってしまいます。この欠損している部分のデータさえ入手できれば、真の治療効果を測定することができるようになります。
治療を受けた群と受けなかった群において、血圧に影響を与える全ての因子が同じ分布をしていたら、例え「?」だらけの表であっても真の治療効果を推定することができます。2つのグループで、血圧の規定因子の中で唯一の違いが降圧薬服用の有無であれば、単純に観察されたアウトカム(Observed outcome)の差を取ることで、真の治療効果を正しく(バイアスなく)推定することができます。一方で、アウトカムに影響を与える因子が2グループ間でバランスが取れていなかった場合、観察されたアウトカムの差を取っても、真の治療効果の推定を行うことができなくなります。
例えば年齢の分布が違っていたとしましょう。一般的に、年齢が上がるほど血圧は上がることが知られています。降圧薬を服用したグループの平均年齢が50歳、服用しなかったグループの平均年齢が70歳であったとします。そうすると、降圧薬を服用しなかったグループの血圧の平均が、治療群よりも高いのは、降圧薬の効果なのか、年齢の影響を見ているだけなのかが分からなくなってしまいます。もし年齢が降圧薬を飲むかどうかの決定にも影響を与えている場合、年齢は交絡因子(Confounder)と呼ばれます。交絡因子とは、治療(疫学では暴露と呼ばれます)とアウトカム(結果)の両方の原因となるもののことを差し、治療効果の正しい推定を妨げる要因となります。
参加者をランダムに治療群と非治療群に割り付けるRCTが優れているのは、測定されていようが、測定されていないとしても、すべての血圧の規定因子が2グループ間で同じ分布をしていることが期待できるという点です。観察研究ではこのバランスが崩れていることがほとんどです。プロペンシティ・スコア法などを使うことで、少なくとも測定されたアウトカムの規定因子に関しては、2グループ間で完璧なバランスを得ることが可能になります。もしアウトカムの規定因子をすべて測定することができてれば、観察研究からであっても真の治療効果を求めることが可能になります。
これはしばしば誤解されていることなのですが、因果関係があることを証明するためには必ずしもRCTを行わなくてはいけないというわけではなく、アウトカムに影響を与える因子が全て測定されていれば観察研究データでも正しく因果推論を行うことができます。もちろん観察研究では測定されていない因子に関する補正を行うことはできませんが、それらがアウトカムに影響を与えていないと自信を持って言うことができるのであれば、無視しても構わないからです。


たいへん分かりやすい説明 ありがとうございます
いいねいいね
Katsu様、コメントありがとうございます。今後ともよろしくお願い致します。
いいねいいね