疑似実験（Quasi-experiment）と観察研究（Observational study）との定義はあいまいですが、ここでは経済学での用いられ方を考慮して、因果推論をきちんと行うことのできる比較的質の高い解析方法を疑似実験として、それよりは弱い研究デザインを観察研究とさせて頂きます。

疑似実験（Quasi-experiment）

1. 操作変数法（IV; Instrumental variable methods）
2. プロペンシティ・スコア・マッチング（PS; Propensity score matching）
3. 回帰分断デザイン（Regression discontinuity method）・分割時系列デザイン（Interrupted time-series analysis）
4. 差分の差分（DID; Difference-in-difference）

本日は操作変数法（IV法）に関してご説明します。前のブログでもご説明したとおり、測定（観察）されていない交絡因子（unmeasured confounders）に関しても対処することができる方法論はRCT、IV法、回帰分断デザインの3つだけです。RCTとIV法以外の研究デザインに関しては、測定されている交絡因子には対処できますが、測定されていない交絡因子に関しては無力です。

治療（暴露）因子の規定因子ではあるものの、アウトカムには治療因子を通してしか影響を与えないものを操作変数（IV）と呼びます。このIVを利用することで、治療因子のアウトカムへの影響を評価する方法がIV法になります。医学の領域では、心血管カテーテルのできる病院から自宅の距離などがIVとして用いられています。病院からの距離が近いほど心血管カテーテルを受ける確率が高くなり、遠いほどその確率は低くなります。一方で、病院からの距離は少なくとも直接的には心筋梗塞患者の予後に影響を与えないと考えられます。もしこれらの仮定が成り立てば、病院からの距離をIVとすることで、心血管カテーテルの患者の死亡率への影響を評価することが可能になります。IV法を用いることで、測定された交絡因子と測定されていない交絡因子の両方に対応したことになります。この話だけ聞くとIV法が素晴らしく優れた研究デザインのように聞こえると思いますが、IV法が成り立つためには4つの条件を満たす必要があります。この中でも一番重要なのは（１）Exclusion restrictionと（２）No instrument-outcome confounderの2つですが、まずは4つの条件を順番に説明していきたいと思います。

IV法が成り立つための条件*

1. Exclusion restriction：IVが直接アウトカムに影響を与えることはなく、IVは治療因子を通してしかアウトカムに影響を与えない。
2. No instrument-outcome confounder： IVとアウトカムの両方に影響を与える「共通の原因（Common cause）」が存在しない
3. Instrument relevance（操作変数の関連性）: IVはきちんと治療因子に影響を与える（IVが治療因子を強く予測する）
4. Monotonicity： IVが治療効果に逆効果になる人たち（Defiersと呼ばれる人たち）がいない

このうち（３）は比較的簡単に評価することができます。IVと治療因子（T）との間の相関関係を見ます。この場合、統計学的に有意かどうかに加えて、相関の強さが重要です。IVが治療効果を予測する力が弱い場合（Weak instrumentsと呼ばれます）、仮にバイアスがあった場合にそのバイアスを増幅してしまうことが知られています。一般的には、F-statisticsが10未満であると問題であるとされています（Staiger and Stock, 1997）。

（４）MonotonicityとはIVが治療効果に対して逆効果にならないという仮定です。下記のように4つのグループの人たちがいるとします。この中でComplierとはIVの影響に従って治療を受けるかどうか決める素直な人たちです。一方で、Defierとは一般的にIVから期待される治療効果への影響に逆らった行動パターンを取るあまのじゃくな人たちのことです。そして、Monotonicityの仮定とは「Defierがいないこと」になります。

Complier（従順な人たち）	IV=1ならT=1となり、IV=0ならT=0となる「素直に従う人たちのこと」
Defier（あまのじゃくな人たち）	IV=1ならT=0となり、IV=0ならT=1となる「ひねくれもの」
Never-taker（常に非治療群）	IV=0であると1であろうと、常にT=0である人たち
Always-taker（常に治療群）	IV=0であろうと1であろうと、常にT=1である人たち

IV法で推定することのできる治療効果はLATE (Local average treatment effect) もしくはCATE (Complier average treatment effect) と呼ばれるものです。ランダム化比較試験では、グループ全体が治療を受けた場合と、グループ全体が治療を受けなかった場合との差が治療効果になります。それに比べて、IV法で推定される治療効果は、グループ全体ではなく、上記のテーブルのComplier（従順な人たち）における治療効果になります。よって、IV法で得られた治療効果と、ランダム化比較試験から得られた治療効果を横並びで比較することはできません。一般的に、LATEはランダム化比較試験で得らる治療効果よりも大きい値になる（0からより離れた値をとる）ことが知られています。

IV法の一番の問題はデータなどからは評価することのできない問題があることです。その中でも（１）と（２）が最も問題です。ちなみにInstrument-outcome confounderとは後述するGarabedianとSoumeraiらの論文で使い始めた表現ですので、一般的に広く使われている表現ではありませんので注意して下さい。この（１）と（２）を組み合わせてExclusion restrictionという表現することもありますし、Instrument exogeneity（操作変数の外生性）と呼ぶこともあります。イメージ図で表すと、（１）はこちらのような関係であり、

（１）Exclusion restriction

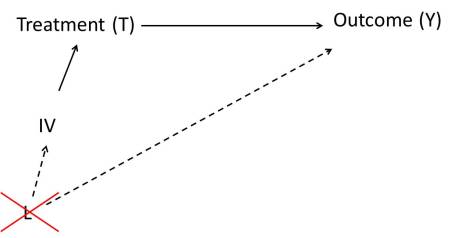
（２）はこのようなイメージになります。この場合、LはIVとアウトカムの共通の原因（Common cause）であり、交絡因子となります。

（２）No instrument-outcome confounder（図中のL）

仮にIVが直接アウトカムに影響を与えていないと信じるだけの十分な根拠があるとしても（データでは確かめることができないのでメカニズムから考察する必要があります）、（２）のように第三の因子がIVとアウトカムの共通の原因（交絡因子）になっているときにもIVの妥当性は崩れてしまいます。実際には巷にあるIVを使っている研究のほとんどがこのIVとアウトカムの交絡因子をきちんと考慮されていないことがGarabedianとSoumeraiらの研究でも証明されています。私自身も、RCTやくじ引きを除いては、理想的なIVとはいまだかつて出会ったことがありません。経済学者にどのようなIVが信頼できるか？という質問をぶつけても、ほとんどの場合でRCTやくじ引きという答えが返ってきます。ちなみに経済学者はRCTにおける「治療の割り付け」も一種のIVであると捉えています。この場合には、治療の割り付けはランダムに行われていますので、IVはアウトカムに直接影響を与えなく、IVとアウトカムの共通の原因が存在しないという条件をきちんと満たしており、完璧なIVであると言うことができます。

*IV法を用いて局所的平均処置効果（Local average treatment effect； LATE）を推定するためには、この4つの条件に加えて、SUTVA（Stable Unit Treatment Value Assumption）と呼ばれる条件も満たす必要があります。SUTVAは次の2つの条件からなります。1つ目は、ある被験者に対する介入の有無は、他の被験者の潜在的なアウトカムに影響を与えないという条件です（Non-interference）。つまり、データに含まれる被験者がお互いに独立している（周囲の人への波及効果が無い）ということを意味します。2つ目は、受ける介入の詳細（用量や種類など）は被験者によって異ならないという条件です（No variation in treatment）。例えば、ある薬の介入効果の評価をしていた場合、人によって薬の用量や種類が異なるといったことが無いということを意味します。

さらに疫学では、同質性（Homogeneity）、つまりIVが、原因と結果の関係性を変えないことも満たすべき条件であると最近では考えられるようになってきています。疫学の世界では、遺伝子多型をIVとして利用する（例えばアルコールに強い遺伝子をIVとして利用することで、飲酒と健康の関係を評価します。多くの場合では遺伝子に影響を与えるような因子が存在しないため、遺伝子は理想に近いIVであると考えられています）ことで因果関係を明らかにしようとするメンデルランダム化解析（Mendelian randomization）と呼ばれる研究手法があります。この手法を用いた研究の中で、原因となる因子と関連する遺伝子によって、原因と結果の関係性が変わってしまうことがあることが明らかになっています。